297. 二叉树的序列化与反序列化

发表于 分类于 阅读次数： 本文字数： 831 阅读时长 ≈ 3 分钟

昨天看到这道题目，我有点头皮发麻，主要是想到了字符串的处理，不过，我想到，既然要写算法，怕麻烦的心态不能有，算法题再麻烦，能有业务麻烦？

对一个二叉树进行序列化，其实就是把一个非线性的数据结构，转化成线性的数据结构。比如，我们按照某种顺序去遍历二叉树，就会把二叉树转换成一个序列，就相当于序列化了。我们可以使用：

  1. 前序遍历
  2. 中序遍历
  3. 后序遍历

反序列化是什么呢？就是从一个给定的序列，恢复出原来的树。这个过程毛想想可能有点麻烦，不过真写出来，其实又不那么麻烦了。

先来说序列化的部分。我们选择前序遍历作为序列化的方法：

1
2
3
4
5
6
7
8
9
10
11
def serialize(self, root):
    res = []
    def _serialize(tree):
        if not tree:
            res.append('None')
        else:
            res.append(str(tree.val))
            _serialize(tree.left)
            _serialize(tree.right)
    _serialize(root)
    return ','.join(res)

我使用了一个内部函数，用一个变量 res 来存储结果数组，然后内部函数是一个递归前序遍历算法。这里注意的主要就是根节点被表示成了 None，也可以是别的，等会儿反正反序列化的时候，你照着反解就行了，这其实就是所谓的“协议”了。

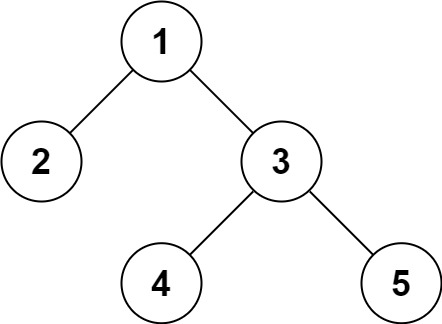
二叉树的例子

对于图例里的二叉树，我们前序遍历后，得到的是什么呢？

1
1, 2, None, None, 3, 4, None, None, 5, None, None

接下来说反序列化，可能，这是大家可能会觉得难的部分，因为每次看到二叉树这个主题，研究怎么遍历这个树的次数，要远远多于研究怎么构建这个树的次数，所以，当我们想从一个字符串构建这个树的时候，就会感觉陌生，从而提高了难度。

我也是实际写了一下，才发现，好像写出来以后，也并不是很复杂。我写了一个递归方法，方法的功能是：把输入的序列当成一个前序遍历结果，然后返回恢复后的树的根。递归方法的构造过程很有意思，就是我们总是先假设我们已经写出了这个函数，再去写这个函数。有点像哆啦A梦穿越时空的糊涂账。这也就是递归有趣的地方。

二叉树为什么这么有意思？因为二叉树也是个典型的递归结构。一棵二叉树和这棵树的左右子树，在性质上是完全一样的东西，只是差了一层而已。

当我们恢复一个前序序列为树的时候，我们知道，第一个元素是根节点，然后，后面就是左子树，然后再后面是右子树，恢复左子树的时候，就可以递归使用自己来完成了，所以根本不用头疼后面怎么办，也不用头疼左右子树的分界点在哪里这种问题了，毕竟“我们已经写出了这个函数”，对不对？哈哈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def deserialize(self, data):
    l = data.split(',') # 字符串切割成列表
    i = 0               # 遍历列表的下标指针
    def _deserialize():
        nonlocal i # 解决 Python 的闭包问题
        if l[i] == 'None':
            i += 1
            return None
        root = TreeNode(int(l[i]))  # 第一个遇到的元素是根节点
        i += 1                      # 元素用掉后，下标后移
        root.left = _deserialize()  # 递归构造左子树
        root.right = _deserialize() # 递归构造右子树
        return root
    return _deserialize()

写完后，才发现，很意外，这个反序列化的方法，几乎和序列化一毛一样，也是一个前序遍历的递归过程。

好，到这里，序列化和反序列化就都写完了。还蛮有趣的。

  • End -