用状态机实现《394. 字符串解码》
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = “3[a]2[bc]”
输出:“aaabcbc”示例 2:
输入:s = “3[a2[c]]”
输出:“accaccacc”示例 3:
输入:s = “2[abc]3[cd]ef”
输出:“abcabccdcdcdef”示例 4:
输入:s = “abc3[cd]xyz”
输出:“abccdcdcdxyz”
- 字符串解码 --> 传送门
今天做到这么一道题目,这个题目我一看,就想起了大学时候学习的编译原理,这个字符串解码,显然是“一个语言”,只不过这个语言的语法特别简单,只有字母,中括号和数字。我们要实现的就是,做一个这个“语言”的解释器,然后打印语句的结果。
既然是语言,我们就按照语言的方式来解决。这个语言里,只有四种 TOKEN(这是个专有术语),数字,左中括号,右中括号,字母,很容易划分 TOKEN,因为每种 TOKEN 的边界都是不同的字符。
语法非常简单,就是数字用于修饰一个字母串,中括号用于分割被修饰的字母串。只有唯一的操作,就是“打印”,有两种状态,“直接打印”,“重复打印”。于是我画了一个状态机:
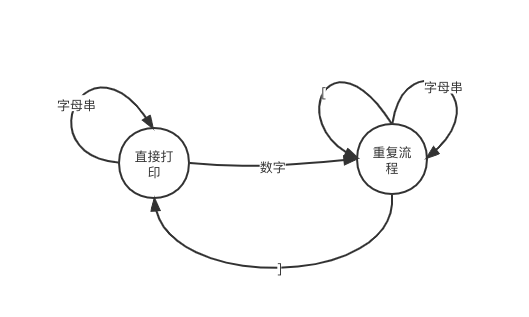
状态机
在初始状态下,遇到字母就直接打印,遇到数字,马上进入重复打印的流程,遇到右括号的时候,开始将遇到的模式重复打印。并退出重复打印的流程。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19def decodeString(self, s: str) -> str:
res = ''
count = 0
p = ''
state = 'print'
for c in s:
if state == 'print' and ord('a') <= ord(c) <= ord('z'):
res += c
elif ord('1') <= ord(c) <= ord('9'):
count = count * 10 + int(c)
elif c == '[':
state = 'start'
elif c == ']':
res += p * count
count, p = 0, ''
state = 'print'
elif state == 'start' and ord('a') <= ord(c) <= ord('z'):
p += c
return res
写出来一测,我才发现,原来括号是可以嵌套的。上面的代码对于嵌套的括号是没法正确处理的。并且通过编写这个代码,发现我识别的两个状态似乎也有点错误,这个语言太简单了,状态的切换也有点多于。
我发现,整个“语言”其实是一个递归的结构,可以表达成 “字母串 = 字母串 + 字母串 × 重复次数”,中括号其实就是字母串的分割边界。每遇到一个左括号,字母串的处理就深入一层,遇到一个右括号就跳出一层,只要用一个栈就可以轻松解决了。栈里要记录的东西,其实就是外层的前面一半字母串,以及内层需要重复的次数。这样,代码就改成了:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16def decodeString(self, s: str) -> str:
res = ''
count = 0
stack = []
for c in s:
if ord('a') <= ord(c) <= ord('z'):
res += c
elif ord('0') <= ord(c) <= ord('9'):
count = count * 10 + int(c)
elif c == '[':
stack.append((res, count))
res, count = '', 0
elif c == ']':
ctx_res, ctx_count = stack.pop()
res = ctx_res + res * ctx_count
return res
反倒更简洁了,我们需要求的是最外层的字母串,遇到左括号就压栈,遇到右括号,出栈的同时,做重复计算。栈里保留了当前字母串需要重复的次数。
这个算法的时间复杂度是O(n),空间复杂度也是O(n)。当然,到这里,想要写出这个算法的递归算法也是非常简单:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20def decodeString(self, s: str) -> str:
def process() -> str:
nonlocal i
res = ''
count = 0
while i < len(s):
c = s[i]
i += 1
if ord('a') <= ord(c) <= ord('z'):
res += c
elif ord('0') <= ord(c) <= ord('9'):
count = count * 10 + int(c)
elif c == '[':
res += process() * count
count = 0
elif c == ']':
return res
return res
i = 0
return process()
– END –
