WordPress 数据库损坏
常在河边走,哪能不湿鞋。没想到,从 2008 年开始深入玩 WordPress 博客到现在,竟然第一遇到了数据库损坏,真是闻所未闻,见所未见啊……一个个人博客而已,毫无访问和压力,竟然也可以搞成这样。
常在河边走,哪能不湿鞋。没想到,从 2008 年开始深入玩 WordPress 博客到现在,竟然第一遇到了数据库损坏,真是闻所未闻,见所未见啊……一个个人博客而已,毫无访问和压力,竟然也可以搞成这样。
作为程序员工作十几年了,Shell 编程这项技能,就好像“你永远得不到的爸爸”一样,每次想用的时候,都觉得自己从来没学会过。本文的编写作为一篇学习笔记,或者一个备忘录,或者一个作弊小抄,我会在每次遇到的时候,不断前来添砖加瓦,说不定有朝一日,能有望凑成一本秘籍。虽然网上类似的内容很多了,但是那些终究是别人的东西,自己用着总是不得劲,所以,做笔记这项技能总是伴随着人类的发展。
大家有没有发现,有些技术点,我们每次想用的时候,都不会用,然后学会了,用一次,又很久不用,然后到了要用的时候,又开始新一轮的循环。比如 git 的 submodule,对我来说就是这样一个技术点。
PopClip 是我非常喜欢也非常依赖的一个软件,属于 “润物细无声” 这个类目的软件。
软件的功能是,当你用鼠标选中一个文本的时候,弹出来一个浮动菜单,提供一系列的快捷小功能。缺省的功能有,搜索引擎,相当于划词搜索,还有字典查询,可以立刻激活系统的字典,还有拼写检查等。
指令式编程,Imperative Programming,是一种编程泛型,通过编程指令,告诉计算机,每个步骤执行的命令,计算机按照代码的指令,逐行执行,就能得到最终结果。
指令式编程的优点是非常符合直觉,代码发出命令,计算机执行。所以,这种编程泛型也非常容易学习,我们入门学习的 C 语言,Java 语言等等,都是支持指令式编程的,也是这类语言的主要编程泛型。
面向对象编程,也是一种编程泛型,同时,面向对象编程泛型,也是一种指令式编程泛型的特例。所以,指令式编程,是一个更抽象的概念。
声明式编程,Declarative Programming,顾名思义,这种编程泛型,更倾向于告诉计算机,“是什么”,由计算机自行决定如何操作。
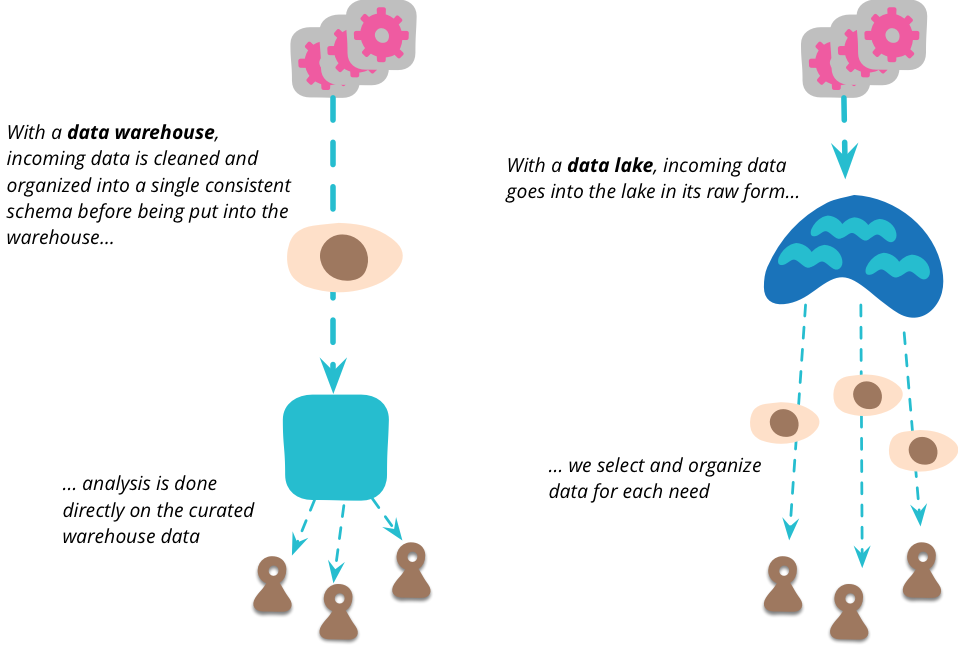
邮箱里看到了技术文章推送的邮件,提到了数据湖、湖仓一体等等概念,我有点好奇到底是什么东西。
初步看了两篇文章,我感觉,这个“数据湖”又是一个热门潮流概念吧。没想到 Martin Fowler 大叔也撰文专门描写了数据湖。
“回溯法”(Backtracking)和“深度优先搜索”(Depth First Search-DFS),看起来名字截然不同,字面意思也没什么相似的,不过,如果你经常刷题,渐渐就不免会注意到这个问题。为什么这两者会凑到一起去了?
我最早注意到这个问题,是观看题解的示范代码,示范代码是一道使用“回溯法”解决的题目,可是很奇怪,函数却并命名为 dfs,明明是回溯法,怎么用 dfs 来命名函数呢?为啥不用 backtracking 命名函数呢?
Backtracking is a general algorithm for finding all (or some) solutions to some computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions, and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot possibly be completed to a valid solution.
回溯法是一种通用的算法,用于找到一些计算问题所有的(或者部分的)解,尤其是约束满足类问题,该算法逐渐构建潜在的解,一旦确认潜在的解无法满足,则立刻抛弃。
回溯法一个最经典的例题是“八皇后”问题,在一个国际象棋棋盘上,尝试放 8 个皇后,这 8 个皇后不能互相攻击,尝试找到一种或所有的解。8 个皇后不能在在同一行,同一列,或者同一对角线上。
回溯法解题的步骤大概是,首先在第一行挑选一个位置防止一个皇后,然后在第二行,放置皇后的时候,就不能产生攻击,一旦发现第 8 个皇后已经放置完毕,则搜索到了一个解。如果还没有放足 8 个,就发现已经无处可以放置了,则返回上一行,将上一行的皇后换一个位置放置(回溯)。
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
深度优先搜索,是一种用于遍历或者搜索树或者图数据结构的算法。算法从树的根节点开始(或者图的任意节点),然后沿着连接节点的边,尽可能深的遍历图,直到回溯。
在深度优先遍历的定义里,出现了回溯这个词。不难想象,假设有一颗树,我们从根节点开始深度优先遍历,那么会从根节点,一直向下深入,直到叶子节点,这时候如果想继续遍历,则必须返回父节点,这样才能寻找兄弟节点进行遍历。这个“返回” 的过程,就根回溯极其类似。
结合维基百科的定义和两个算法的基本描述,我们不难发现这两个算法的相同之处,通俗点说,都是选定一种策略,一条路走到黑,如果走入死路,就退回来,重新选择。
这“两种”算法的另一个相同之处是,都是遍历解空间的一种策略,说直白点,都是“穷举”的算法,只不过,穷举解空间也好,穷举图也好,都需要选定一个策略,才能没有遗漏和没有重复的完成穷举。
所以,我自己更倾向于认为,这两者,其实是同一种算法,只是从不同角度出发去称呼他们。事实上,我打开了好几本中文版算法书,《算法 4》,《算法导论》之类的,《算法竞赛入门经典》《算法竞赛进阶指南》等等,几乎就没找到过关于“回溯法” 的介绍和定义。难怪那些搞竞赛的,遇到回溯法,都会用 dfs 去命名函数。
通过在 StackOverflow 搜索,还真有人问这个问题。
For me, the difference between backtracking and DFS is that backtracking handles an implicit tree and DFS deals with an explicit one. This seems trivial, but it means a lot. When the search space of a problem is visited by backtracking, the implicit tree gets traversed and pruned in the middle of it. Yet for DFS, the tree/graph it deals with is explicitly constructed and unacceptable cases have already been thrown, i.e. pruned, away before any search is done.
So, backtracking is DFS for implicit tree, while DFS is backtracking without pruning.
这个回答认为,回溯法,处理了隐式树,而 DFS 则处理显示的树。这看起来平凡,但是也意味深长。当使用回溯法遍历一个问题的搜索空间时,隐式树在遍历的过程中,进行剪枝。但是,DFS 算法则不同,显示的树或者图已经被构造出来了,那些不可达的节点,或者不可能的情况,此时已经被排除在外了,只要按部就班全部遍历即可。所以,他认为,回溯法就是隐式树/图的深度优先搜索,而 DFS 就是没有剪枝的回溯法。
当然,也有很多回答认为是两种不同的算法,只是我比较倾向于这个答案。也有从字面去解释的,我觉得也可以听听,比如有人说,回溯法是解决问题的方法论,而 DFS 是算法。隐式图,显示图什么的,也不那么难以理解。事实上,我认为现实世界里,只有隐式图,真正的显示图是很罕见的。正因为我们对现实世界进行了抽象,才出现了显示图这种东西。
比如,使用回溯法常见的一类问题就是排列组合问题。例如经典的,使用 n 对括号,能排列出多少种合法的括号串(括号必须配对)。这是经典的需要回溯法解决的问题,你能把这个问题想象成图么?不管如何,如果你能把这个问题写成一个递归函数来解决,至少在递归深入到下一层和回来的过程,都绘制成节点和边的话,这个可视化出来的东西,就是一棵树(树是图的特例)。
所以,不用在纠结“深度优先搜索”和“回溯法”有什么区别了,只要知道,这两者就是一体两面,或者你认为根本是一回事也不为过。显示图和隐式图也没任何区别。只是隐式图更贴近显示世界,而显示图更贴近抽象世界。如此而已。
刷题到现在,不知不觉过了 500 大关后,真的不能再随随便便了,要认真起来了。就好像写博客,坚持了几年后,你就不自觉地内化了这个行为,好像自己隔了一段日子,就一定要写点什么了。
之前 500 纪念的文章里,也说了,明确感受到了瓶颈。好像自己刷题没什么长进了。幸好一个朋友提点,要逐个点击破来提高了。这两天就开始留意了。方法很简单,就是之前不会做就跳过的东西,现在就要求自己一定要看懂,不能随便跳过任何东西。不惜代价也要搞明白再往后。就发现,其实自己掌握的东西还是千疮百孔的。
其实目标是最重要的东西,就是到底想通过刷题获得什么?这样才能决定做法。如果说,刷题是为了找工作,应该刷《剑指》,反反复复刷,知道随机跳题都能秒做对。当然,这不是我的目标,因为之前也说了,35+ 找工作的时候,刷题只是获得一个聊天的机会,并不能帮助我了。
我现在定个小目标是,能在周赛妥妥 3 道题。很多同学可能觉得这很容易,当然我打心眼里也没觉得有多难,所以只能是一个小目标了。只是,以此为目标的时候,我能清晰定位到,自己缺少多少知识。也是自己之前可以忽略的东西。
当然,短板还是有很多很多的,只是这几个是我目前想到的,欠缺比较多的东西,如果有针对性地训练的话,可能会有比较大的成效,也即在这些领域投入,边际效益会大一点。那就把这几个定成这一轮的焦点问题,尝试比较集中去投入一些经历。
目前,在参加一个 91 天学算法训练营,花了 10 块的,群里的人感觉比较基础,自理能力也一般,经常还在问群主一些网站登录不了怎么办的问题,GitHub 没法访问的问题。每天的题目按照数据结构的顺序在出,不过呢,几乎都没有挑战了,打算就做着每日打卡权当是查漏补缺了。
LC 的每日打卡还是要坚持打的,因为几乎可以认为是随机在跳题出来的,这样比较容易发现自己的短板的。
此外,还是应该找专题来做,集中攻破一个个点。然后,三到六个月来回顾。
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
- 最长递增子序列 <-- 传送门
这道题目是一道非常经典的基础算法题。
一个数组里包含多少个子序列呢?按照数组原有的顺序,每个元素我们可以选择删除或者保留,最后形成的序列,就是一个子序列。每个位置有“删除”或“保留” 2 种情况,所以,穷举的话,总共有 2^n 个子序列。
这些子序列的长度,从 0 到 n 不等,我们现在想求出,子序列中元素严格递增的序列,最长的长度是多少。不难得到,最短的严格递增子序列长度是 1,最长的可能性是 n。也同样不难想象,某一个长度的严格递增子序列,不止一条。
我们尝试使用递归法,来设计一个算法,求解这道题。下面是推理过程:
步骤 1,递归假设。我们直接假设,可以求出长度为 n 的数组的最长递增子序列的长度,也即最终答案,用 f(n) 表示。
在这个基础上,我们来考察第 n + 1 个数,我们能否使用 f(n) 计算出来。一个数字能不能让一个递增序列的长度 +1,取决于这个数字是否大于序列中最大的数字(因为是要保持数组的原有顺序,不用考虑这个数字是否小于最小值的情况)。现有递归假设,不包含那个最大值,所以假设失败。
增强假设。我们除了能计算出最长子序列的长度,我们还能计算这个子序列的最大值。考虑到,同样长度的子序列很多个,那么这么多子序列的最大值,我们返回哪个呢?稍加思考,发现,我们可以返回这里最小的一个,记为 Xs。因为新来一个数字,只要比 Xs 大,就可以让最长子序列的长度 +1 了。
在新的假设基础上,我们考察第 n + 1 个数,如果这个数字大于 Xs,那么 f(n+1) 的最长子序列,就是 f(n) 的最长长度 +1。那么,新的最长子序列的最大值是多少呢?显然也是第 n + 1 个数。可是如果第 n + 1 个数,小于 Xs 怎么办?假如 f(n) 计算的最长子序列长度是 L,最大值是 Xs,第 n + 1 个数字小于 Xs,但是比长度 L-1 的子序列的最大值要大,就可以得到另一条长度 L 的子序列,那条子序列的最大值是第 n + 1 个数,这种情况,需要更新 Xs 为第 n + 1 个数。那还是同样的问题,如果小于又怎么办呢?还要用同样的办法再向前探索 L-2 的子序列最大值。
这一部分稍微有点点抽象,但是细想一下不难理解的。所以,我们目前的假设,还是不够强。
继续增强假设。假设我们能计算出,长度从 1 到 L 的每种长度的子序列的最大值(里面的最小的一个)。
在这个最新的假设下,考察第 n + 1 个数。通过第 n + 1 个数与整个数组的每一个数,从后往前逐个判断,就能决定是追加到最后面,还是替换其中的一个。不难证明,返回的这 L 个数字,是从小到大严格递增的(所以可以用二分法找到替换的位置)。最后这个数组的长度 L 正是最后的答案。
基于上面的推理,我们写出递归算法:1
2
3
4
5
6
7
8
9
10
11
12
13class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
def lis(i: int) -> List[int]:
if i == 0: return [nums[i]]
res = lis(i - 1)
# 以下使用二分法,确认替换的位置
j = bisect.bisect_left(res, nums[i])
if j == len(res): # 比最大的还大,就追加到末尾
return res + [nums[i]]
else: # 否则就替换
res[j] = nums[i]
return res
return len(lis(len(nums) - 1)
算法复杂度分析,每一轮递归里,问题规模减小 1,总递归 n 层,并且每层进行了一次二分查找。所以总时间复杂度是 O(n logn)。空间复杂度是 O(n)。
通过递归假设和不断增强假设,我们设计出了递归算法来求解最长递增子序列。这道题也可以很轻松写成迭代的写法,请读者自己动手完成。
当然,这也是一道典型的动态规划的题型,可以用动态规划来求解。假设我们可以设状态为以第 i 个数字结尾的最长子序列,长度为 Li。对于第 i + 1个数字,我们可以检查每个数字 i ,如果大于它,新子序列的长度 Li + 1,这里的最大值就是以第 i + 1 个数字结尾的最长递增子序列长度。
因为,最长子序列不一定是以哪个值结尾的,所以最后整个 dp 数组的最大值就是最终答案。
写出代码就是:1
2
3
4
5
6
7
8class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
dp = [1] * len(nums) # 不难想象,最短的递增子序列长度是 1,当作初始值
for i in range(1, len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
该算法的时间复杂度是 O(n^2),因为每个数字,我们都要考察前面所有的数字的情况。空间复杂度是 O(n)。
– END –