刷完 500 题!偷偷纪念一下吧
又有许久不曾写过题解了,题目一直还在做着,就是懒得写题解,主要最近家里事有点让我烦心,心绪不宁无法安心写作。今天我猛然一看,统计数字 498 了,赶快找两道简单水题,凑个整,算是突破了 500 大关。当然,这对我个人来说,或者毫无意义,总是一个付出的明证吧。
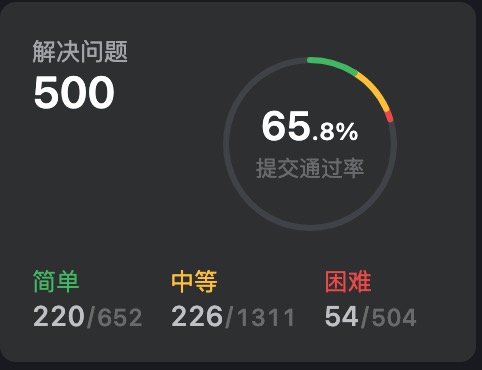
LeetCode 刷题统计
从做题结构看,还是简单题偏多,你就可以想见,这个数字还是挺水的。含金量不像数字那么敦实。花了多久做了这么多题目呢?大概可以认为是 8 个月多吧。

LeetCode 打卡热力图
其实第一次尝试刷题是 2020 年 8 月开始,只在工作日,每天做 1 道,这样坚持了一个半月,放弃了,当时刷了 100 多道吧。今年的 2 月,又开始第 2 波了,上次使用 Go 刷的,这次是用 Python 刷的。两次都重开了做题计划,所以,第二次其实是把第一次的题都又做了一遍的。即这 500 题有 100 多道我是用 Go 做过一遍的。
如何看待刷题这个事情?
刷题大体来说还是快乐的,因为简单。这话不是凡尔赛,真实的个人体会。题目都是那么纯粹,有些题甚至是为了做题而出题,就更显得纯粹。你不懂的时候,可能会让你暴躁得抓头发,那只能是你的见识太少了。因为这些题并不难,只是没见过而已。
比起生活中遇到的那些无解的困难,比起工作上的这些困境。刷题相比之下只是一个纯粹而快乐的过程。刷题不能解决我的问题,但是可以让我从痛苦的生活中逃离一小会儿,用能获得的进步给自己一点点安慰。我想这和那些沉溺在游戏里打怪的人没有太多的区别,只是这个上瘾程度有限。
刷题有什么好处?
我加过各种群,自己也有个小群,都是大家一起刷题的。大部分人比我年轻 10 岁以上。对他们来说,刷题是很实在的,因为现在找工作,想去个好点的公司,都要考算法题的。刷题最大的好处是,让大家有所准备,能够胜任 Code Challenge,获得心仪的 offer,确实还是有效的。
于我而言,只是增加了我的些许自信。毕竟刷题不是面试的全部。对我来说,更大的好处是,增加了我日常工作中解决难题的信心。我们都知道,工作中可能没有算法题,不过工作中可能会有很多很麻烦的场景。那不是说问题多困难,就是十分麻烦,我感觉刷题训练让我更加耐烦。
会让你写麻烦烧脑,容易写错,难于调试的场景时候,更有信心一点,即使写不出来,也不会气恼,删掉重写就是,这种打击在刷题的过程中早已习惯了。
刷题有什么诀窍?
没有太好的。很多同学分享经验我都看了。有几个,我觉得挺认同。刷题呢,不要纠结于非要自己做出来,刚开始很多同学就会沉溺在这个误区里。看题解不丢人。其实这是非常重要的一点,很多人比如我,很晚才领悟这一点。
刷题呢,专项密集训练效果是不错的,就是把相近题,相同考点的题,堆在一起,一顿猛刷,这样效果好。一个主题完了,再去下一个主题。不是随机拉个单子刷,那样效果不好。举个不恰当的例子吧,比如你去健身房健身。你可能会看到眼花缭乱的器械。不过你请过教练,你就会发现,那么多器械,只是少量几个跟你有关。你每次去用的器械不会超过三种。这次去,深蹲,腿弯举,腿屈伸,倒登机。全部虐腿。下次去了,高位下拉,悍马机,引体,全是虐背。刷题也差不多,这个礼拜全是位运算,下个礼拜全是动态规划。
刷题呢,也会倦怠,需要休息。我第一轮刷题,什么都不懂的,就天天随机做,当时不懂回溯,就死磕了几天回溯,连续做了十几道,然后有点感觉了。第二轮刷题,隔了三四个月多吧,我发现但凡看到题目可能可以用回溯解的,我似乎都有点感觉,写个回溯也自然了许多。可见知识技巧,需要沉淀和发酵,有时候你需要的时间地积淀。一顿猛学后,休息几个月,捡起来,反倒觉得似乎脑袋更清楚了。
刷题呢,反复做相同的题目也是有效果的。比如,你看我做了 500 题,其实这里,很多题是做了不止一遍的,其中有一道题,我看到自己有 7 次正确的提交,都在不同的日期里。有不少同学分享经验,按照一些榜单去刷,比如 Hot 100 列表啊,Top 200 列表啊什么的。还有学习专区,有很多专项,动态规划,二分法,堆等等,专项里和列表里,重复其实很高的。但是你重复做也不用担心的,你再次遇到的时候,还真的未必会做的。我们掌握的知识可能没有自己想象的那么扎实。一些很基础的题目条件反射秒写对后,你才能在一些复杂的场景下,水到渠成写出来。再举个不恰当的例子就是,你盖房子的时候,砖块水泥沙子钢筋,最后房子塌了,你怎么确定砖块的问题,还是钢筋的问题,还是你房子结构设计的问题?谁的错?最后可能是沙子用得不够。所以反复做一些基础题,做到倒背入流随手就来,你就知道你的房子砖块水泥都没问题,就是结构不对。能帮你快速排除一些错误的猜测。
我现在什么水平?
很遗憾,我还是水平很低的,就好像上面说的,我刷题的结构里,太多简单题了。就是灌水成分大了点。我现在的水平就是简单题,大多数可以想出来,中等题,我大概 70% 把握,困难题,我大概 40% 把握,也即一多半做不出。
前天晚上周六,正好没有双周赛,我就开了个模拟周赛试试。最后 1 个半小时的时候,我做对了两道。又加了 5 分钟,终于第三道做出来了。第四道我都没读题目,时间耗完了。我历史上参加过 9 次周赛,6 次我做出来 2 道,2次只做出来 1 道,还有 1 次做出来 3 道,高兴坏了,那次也是我最后一次参加周赛。
未来
刷题是需要长期坚持的,跟健身又很像,你一顿操作猛如虎,一看效果二百五。还不如细水长流,常年坚持。可能不需要很卖力,就是时不时练练,可以保持健康。在市场不断内卷的当下,保持头脑健康是很重要的。
现在我的水平已经进入瓶颈,每天这么做着也没啥长进。朋友说,你需要画个脑图一个点一个点细细去补那些漏洞了(数据结构和基础算法的漏洞,故意忽略的那些知识点),另外以前不曾踏足的领域也要逐步尝试,拓宽面,这样才可能在竞赛里做出好成绩。总之,是进入了一个边际效益很低的区段了。后续怎么做,还是要看自己的目的,想通过刷题得到什么。
– END –